一个经典概率算法(用于抽奖等场景)

大前端

2020-05-11 · 4459

假设有一个数组[100,400,200,300],它的意思是,总数是100+400+200+300=1000. 取到第一个数的概率是100/1000,取到第二个数的概率是400/1000......代码如下:

function getResult(arr) {
 var leng = 0;
   for (var i = 0; i < arr.length; i++) {
       leng += arr[i] //获取总数
   }
   for (var i = 0; i < arr.length; i++) {
       var random = parseInt(Math.random() * leng); //获取 0-总数 之间的一个随随机整数
       if (random < arr[i]) {
           return i //如果在当前的概率范围内,得到的就是当前概率
        } else {
            leng -= arr[i] //否则减去当前的概率范围,进入下一轮循环
        }
   }
}

下面来解释一下这个算法,把数组抽象出来,假设为a,b,c,d,这四个概率数,那么,他们的总和就是 a+b+c+d. 画成数轴:

从0-(a+b+c+d) 中取一个随机数,数字落在对应的空间里,取到的就是对应的概率.

第一次循环取数,有两个可能:

<a 或者 >a:

如果是第一种可能,那就直接是概率a/(a+b+c+d),得到的对应结果就是a.直接返回.

如果是第二种可能,那么概率应该是(b+c+d)/(a+b+c+d).然后进入第二次循环,第二次取数我们把a的概率空间减去,得到新的数轴:

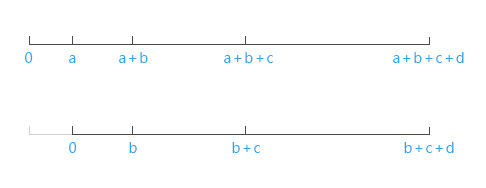
新的数轴以原来的a为原点0,后面不变.这时候,总和变成 b+c+d.

从 0-(b+c+d) 中取一个随机数,数字落在对应的空间里,取到的就是对应的概率.

同样有两个可能:

<b 或者 >b

如果是第一种,那么它的概率就是 b/(b+c+d). 注意,这个概率出现的前提是第一次的结果是 >a ,所以总概率就是两次乘积: (b+c+d)/(a+b+c+d) * b/(b+c+d) 得到的结果是 b/(a+b+c+d),得到的对应结果就是b.返回.

如果是第二种,那么它的概率就是 (c+d)/(b+c+d). 同样,和 >a 的结果同时出现,这种情况的总概率应该是: (b+c+d)/(a+b+c+d) * (c+d)/(b+c+d) 得到的结果是(c+d)/(a+b+c+d).然后进入第三次循环,然后第三次循环时,我们再把b的概率空间减去............以此类推.............

这样直到最后...总能取到一个概率值...

这个算法可以用在抽奖上,比如有这样一组奖品和对应的概率:

var gifts = [{
   "name": "mac",
  "prop": 1
},
{
    "name": "红米",
   "prop": 10
},
{
   "name": "u盘",
   "prop": 40
},
{
   "name": "香皂",
   "prop": 49
}];

//就可以用前面的函数来进行抽奖:
var gArr = [];
for (var i = 0; i < gifts.length; i++) {
   gArr.push(gifts[i]['prop'])
}
console.log(gifts[getResult(gArr)]['name'])

源文件下载:http://pan.baidu.com/s/1oeOG2

转载自：https://www.cnblogs.com/liulangmao/p/4533293.html